2025年1月29日
ポイント
●量子力学の要請を満たす散乱の振幅と確率の計算に成功。
●なぜ短距離ポテンシャル中の連続固有値状態で破られるか、起源、結果と解決法を解明。
●幅広い量子現象の厳密な遷移確率の進展に期待。
概要
北海道大学の石川健三名誉教授（元大学院理学研究院教授）らの研究グループは、量子力学における基本問題であるL^2解に基づくポテンシャル散乱の確率の絶対値を得ることに初めて成功しました。
ポテンシャル散乱は、ミクロな世界の情報を得る代表的な方法ですが、100年ほど前に得られた標準的な公式が使われてきました。これは、古典物理の考えを一部踏襲したものであり、量子力学における厳密なものではありませんでした。このため、限られた状況でしか適用することができず、すべての状況で適用できる確率公式が求められていました。
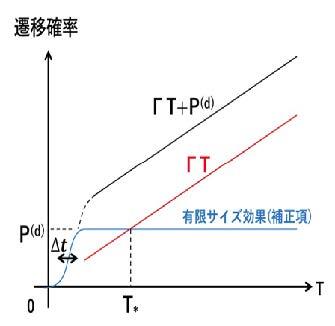
今回の研究は、量子力学の原理に基づいて厳密な散乱の確率を明らかにしたものです。結果には、従来分かっていた項に新たな項が加わっており、幅広い散乱現象が解明できます。始めに、シュレィディンガー方程式の連続固有値解の性質とそれらの内積が明らかにされ、これらに基づいて今までの公式の問題点とその解法が分かりました。その後、遷移確率に関する諸問題が解かれました。その結果、前方領域を含む全領域でのポテンシャルによる散乱確率の絶対値が初めて明らかになりました。
散乱確率の絶対値が分かったことより、未解決な問題の解明が進展すると共に、生物を含む広範囲の科学技術分野への量子力学の応用の道が開かれました。
なお、本研究成果は、2023年12月13日（水）公開のAnnals of Physics誌に掲載されました。
論文名：Potential scatterings in the L^2 space: (2) Rigorous scattering probabilities of wave packets（L^2 空間でのポテンシャル散乱：波束による厳密な散乱確率）
URL：https://doi.org/10.1016/j.aop.2023.169571
詳細はこちら
遷移確率P(T)は時間Tの1次関数であり、切片P^(d)が新しい。
